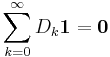Markovian arrival processes
In queueing theory, Markovian arrival processes are used to model the arrival of customers to a queue.
Some of the most common include the Poisson process, Markov arrival process and the batch Markov arrival process.
Contents |
Background
Markovian arrival processes have two processes. A continuous-time Markov process 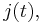 a Markov process which is generated by a generator or rate matrix,
a Markov process which is generated by a generator or rate matrix,  . The other process is a counting process
. The other process is a counting process 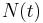 , which has state space
, which has state space 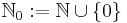 (where
(where 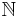 is the set of all natural numbers).
is the set of all natural numbers). 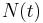 increases every time there is a transition in
increases every time there is a transition in 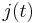 that is marked.
that is marked.
Poisson process
The Poisson arrival process or Poisson process counts the number of arrivals, each of which has an exponentially distributed time between arrival. In the most general case this can be represented by the rate matrix,
In the homogeneous case this is more simply,
Here every transition is marked.
Markov arrival process
The Markov arrival process (MAP) is a generalization of the Poisson process by having non-exponential distribution sojourn between arrivals. The homogeneous case has rate matrix,
An arrival is seen every time a transition occurs that increases the level (a marked transition), e.g. a transition in the 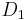 sub-matrix. Sub-matrices
sub-matrix. Sub-matrices 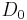 and
and 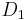 have elements of
have elements of 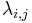 , the rate of a Poisson process, such that,
, the rate of a Poisson process, such that,
and
There are several special cases of the Markov arrival process.
Markov-modulated Poisson process
The Markov-modulated Poisson process or MMPP where  Poisson processes are switched between by an underlying Markov process. If each of the
Poisson processes are switched between by an underlying Markov process. If each of the  Poisson processes has rate
Poisson processes has rate 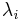 and the underlying process is generated by a
and the underlying process is generated by a 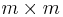 generator matrix
generator matrix  , then in the MAP representation,
, then in the MAP representation,
a diagonal matrix of the rates of the Poisson process, and
Phase-type renewal process
The phase-type renewal process is a Markov arrival process with phase-type distributed sojourn between arrivals. For example if an arrival process has an interarrival time distribution PH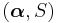 with an exit vector denoted
with an exit vector denoted 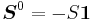 , the arrival process has generator matrix,
, the arrival process has generator matrix,
Batch Markov arrival process
The batch Markovian arrival process (BMAP) is a generalisation of the Markovian arrival process by having arrivals of size greater than one. The homogeneous case has rate matrix,
An arrival of size  occurs every time a transition occurs in the sub-matrix
occurs every time a transition occurs in the sub-matrix 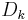 . Sub-matrices
. Sub-matrices 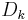 have elements of
have elements of 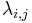 , the rate of a Poisson process, such that,
, the rate of a Poisson process, such that,
and
References
- Søren Asmussen (2000). Matrix-analytic Models and their Analysis, Scandinavian Journal of Statistics 27(2), 193–226.
- David M. Lucantoni (1993). The BMAP/G/1 Queue: A Tutorial, Lecture Notes in Computer Science: Performance Evaluation of Computer and Communication Systems (Editors: Lorenzo Donatiello and Randolph Nelson), volume 729.
- Srinivas R. Chakravarthy (2001). The batch Markovian arrival process: A review and future work. In Advances in Probability and Stochastic Processes, Ed. A. Krishnamoorthy, N.Raju and V. Ramaswami, Notable Publications, Inc., New Jersey, USA, 21-49.
- Srinivas R. Chakravarthy (2010). Markovian Arrival Processes. Wiley Encyclopedia of Operations Research and Management Science. Published Online: 15 JUN 2010.
- Marcel F. Neuts (1992). Models based on the Markovian arrival process. IEICE Transactions on Communications, E75B, 1255-1265.
![Q=\left[\begin{matrix}
-\lambda_{0}&\lambda_{0}&0&0&\dots\\
0&-\lambda_{1}&\lambda_{1}&0&\dots\\
0&0&-\lambda_{2}&\lambda_{2}&\dots\\
\vdots & \vdots & \ddots & \ddots & \ddots
\end{matrix}\right]\; .](/2012-wikipedia_en_all_nopic_01_2012/I/ae6225aa8f42684db5768c1fe10092b3.png)
![Q=\left[\begin{matrix}
-\lambda&\lambda&0&0&\dots\\
0&-\lambda&\lambda&0&\dots\\
0&0&-\lambda&\lambda&\dots\\
\vdots & \vdots & \ddots & \ddots & \ddots
\end{matrix}\right]\; .](/2012-wikipedia_en_all_nopic_01_2012/I/468b7aac816a004fe208733148ff170b.png)
![Q=\left[\begin{matrix}
D_{0}&D_{1}&0&0&\dots\\
0&D_{0}&D_{1}&0&\dots\\
0&0&D_{0}&D_{1}&\dots\\
\vdots & \vdots & \ddots & \ddots & \ddots
\end{matrix}\right]\; .](/2012-wikipedia_en_all_nopic_01_2012/I/5f079744bb42fc530333b5c0261cc99b.png)
![0\leq [D_{1}]_{i,j}<\infty](/2012-wikipedia_en_all_nopic_01_2012/I/5e0d0a3c4317660d821ba7f3075efaad.png)
![0\leq [D_{0}]_{i,j}<\infty\;\;\;\; i\neq j](/2012-wikipedia_en_all_nopic_01_2012/I/9e62b841367c615382a66b6ccf903f5d.png)
![[D_{0}]_{i,i}<0\;](/2012-wikipedia_en_all_nopic_01_2012/I/7b5f0daa455cecce64459dad793a1bfa.png)
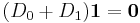
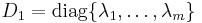
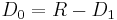
![Q=\left[\begin{matrix}
S&\boldsymbol{S}^{0}\boldsymbol{\alpha}&0&0&\dots\\
0&S&\boldsymbol{S}^{0}\boldsymbol{\alpha}&0&\dots\\
0&0&S&\boldsymbol{S}^{0}\boldsymbol{\alpha}&\dots\\
\vdots&\vdots&\ddots&\ddots&\ddots\\
\end{matrix}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/9321f000afc0535651810ebdbce47ac4.png)
![Q=\left[\begin{matrix}
D_{0}&D_{1}&D_{2}&D_{3}&\dots\\
0&D_{0}&D_{1}&D_{2}&\dots\\
0&0&D_{0}&D_{1}&\dots\\
\vdots & \vdots & \ddots & \ddots & \ddots
\end{matrix}\right]\; .](/2012-wikipedia_en_all_nopic_01_2012/I/d5c44447beaaad330f707ac95b3e1c4a.png)
![0\leq [D_{k}]_{i,j}<\infty\;\;\;\; 1\leq k](/2012-wikipedia_en_all_nopic_01_2012/I/9970b234179ec9556cfd5694514e3590.png)